Coin Toss Probability if Head Roll Die if Tail Flip Again in R
Simulation
Earlier we finish up by analysing your project data, we're going to introduce a few new functions to evidence yous another things that R can do and that volition also reinforce your agreement of probability.
Simulation
1 of the almost powerful features of R is that yous can utilise it for information simulation. Data simulation is the act of generating random numbers that follow a sure distribution or have known properties. This might non sound particularly impressive, but simulating data ways that you can do things such as plan your statistical analyses, empathize and demonstrate how probability works, or approximate how many participants you need to test in your experiment based upon what yous think the data volition look like. Data simulation uses the unlike types of distributions that we covered in Probability to generate data, so brand certain that you're happy with the probability chapter before you move on.
Action 1: sample()
Just like Probability, all the functions we need for simulation are contained in Base R, however, nosotros'll also load the tidyverse and so that we can wrangle our simulated information.
Let'southward start past introducing the sample() office, which samples elements (information points) from a vector (a collection of things that are of the same type, similar numbers or words). Nosotros can utilise sample() to simulate flipping a coin and build some of the graphs you saw in the probability chapter. sample() is used when we want to simulate discrete data, i.e., (nominal or ordinal data).
sample() requires you to define three arguments:
-
10= a vector of elements, i.e., all of the possible outcomes. For our current example, this would be HEADS and TAILS.
-
size= how many samples do you want to take, i.e., how many times do you want R to flip the coin?
-
replace= specifies whether we should sample with replacement or not. In the last lab we used the instance of pulling names out of a hat. If you put the name back in the lid each time yous pulled 1 out this would be with replacement, if you don't put the name dorsum in this would be sampling without replacement. Basically, practise you lot want to be able to get the same event on different samples? For a money flip, it should exist possible to get the same event more than once, so nosotros specifyTRUE. If we specifiedFALSEyou could only depict every bit many samples as at that place were unique values, so in our case we could simply flip the money twice: once information technology would land on heads, once on tails, and then we would run out of outcomes. -
Open a new R Markdown certificate, name information technology "Simulation" and salvage information technology in your Data Skills folder.
-
Copy, paste, and run the beneath code in a new code chunk to simulate flipping a coin four times (and load the
tidyverse).
# Notice that because our consequence labels are strings (text), # we need to enter them into the function in "quotes" library(tidyverse) sample(x = c("HEADS", "TAILS"), size = four, supplant = TRUE) ## [ane] "HEADS" "HEADS" "TAILS" "HEADS" How many heads did you get? Don't worry if information technology'due south different to our instance. Run the code again. How many heads did y'all become this time? How many practice you get on each turn if you run the lawmaking v more times?
When you perform information simulation, you're unlikely to become the same issue each time you take a sample, just like if you flipped a coin 4 times on 5 separate occasions you lot would exist unlikely to get the same number of heads each time. What's so useful nigh data simulation is that we can apply the outcomes from lots of unlike sampling attempts to calculate the probability of a particular result, e.one thousand., getting four heads from 4 flips of a coin.
So that nosotros can add up the number of heads and tails more hands, let's simulate those coin flips once more, but using numerical codes, i = HEADS, 0 = TAILS.
- Now that the outcomes are numeric, we don't need the combine office
c
- 0:1 means all numbers from 0 to 1 in steps of 1. So basically, 0 and 1. If yous wanted to simulate rolling a die, you would write
ane:half dozenwhich would requite yous all the whole numbers from one to 6.
sample(10 = 0 : 1, size = 4, supervene upon = TRUE) ## [ane] ane 1 i 0 Activity 2: sum()
At present that nosotros're using ones and zeroes we can count the number of heads by summing the values of the outcomes. The beneath lawmaking will sample our coin flips every bit above, and and so count up the outcomes. Because we've coded heads = one and tails = 0, nosotros can interpret the sum of all the outcomes every bit the number of heads.
- Copy, paste and run the code below in a new code chunk.
# This lawmaking pipes the output of sample() into sum() which counts up the number of heads/1s. sample(x = 0 : 1, size = 4, replace = True) %>% sum() ## [1] 2 Run this function multiple times (you lot tin use the light-green markdown play arrow at the height right of the code clamper to make this easy). In our simulation of five sets of 4 flips we got 1, iii, two, 2, and 3 heads. And so in only one out of the five simulations did nosotros become exactly one heads, i.e., a proportion of .2 or 20% of the time.
Activity 3: replicate() 1
Let'due south repeat the experiment a whole agglomeration more than times. Nosotros can have R do this over and over again using the replicate() function. replicate() requires 2 arguments (although at that place are other optional arguments if you want to practice more complicated tasks):
-
n= the number of times you lot want to repeat your code
-
expr= the expression, or code, you want to repeat
Re-create, paste and run the below code into a new code chunk to run the sample office and sum upward the outcomes 20 times.
replicate(n = 20, expr = sample(0 : 1, 4, Truthful) %>% sum()) ## [ane] 2 3 1 1 2 i 1 1 0 2 3 4 ii 1 2 3 3 2 iii 3 Monte Carlo simulation
Every twelvemonth, the city of Monte Carlo is the site of innumerable games of chance played in its casinos by people from all over the world. This notoriety is reflected in the utilise of the term "Monte Carlo simulation" amid statisticians to refer to using a figurer simulation to estimate statistical backdrop of a random procedure. In a Monte Carlo simulations, the random procedure is repeated over and once more in social club to assess its performance over a very large number of trials. It is usually used in situations where mathematical solutions are unknown or hard to compute. Now we are ready to use Monte Carlo simulation to demonstrate the probability of various outcomes.
Activity 4: replicate() two
We are going to run our money flip experiment once more but this time nosotros are going to run the experiment 50 times (each including 4 coin tosses), and utilize the aforementioned principles to predict the number of heads nosotros will get.
- Copy, paste, and run the beneath code to run the simulation and store the result in an object `heads50** using the code below:
heads50 <- replicate(50, sample(0 : 1, 4, TRUE) %>% sum()) heads50 ## [1] iii 0 2 1 3 2 0 iii i 4 2 3 2 3 iv 1 1 ii 2 iv 2 3 two three ane 2 2 2 2 ane 4 3 ane 3 3 ane 2 3 ## [39] 1 2 1 iii ii ii 1 two i 3 three two Activity 5: probability
Nosotros tin can estimate the probability of each of the outcomes (0, 1, 2, iii, 4 heads after 4 money tosses) by counting them upwardly and dividing by the number of experiments. We will do this by putting the results of the replications in a tibble() and then using count().
data50 <- tibble(heads = heads50) %>% # convert to a table group_by(heads) %>% # group by number of possibilities (0,ane,2,three,iv) summarise(n = n(), # count occurances of each possibility, p=northward/ 50) # & calculate probability (p) of each | heads | n | p |
|---|---|---|
| 0 | 2 | 0.04 |
| 1 | 12 | 0.24 |
| 2 | eighteen | 0.36 |
| 3 | 14 | 0.28 |
| 4 | iv | 0.08 |
Your numbers may be slightly different to the ones presented in this book - call back that by default, each fourth dimension you run a simulation, you will become a different random sample.
Activity six: visualisation
We tin then plot a histogram of the outcomes using geom_bar().
# Note: stat = "identity" tells ggplot to utilize the values of the y-axis variable (p) as the meridian of the bars in our histogram (equally opposed to counting the number of occurances of those values) ggplot(data50, aes(x = heads,y = p)) + geom_bar(stat = "identity", fill = "regal") + labs(x = "Number of Heads", y = "Probability of Heads in four flips (p)") + theme_minimal() 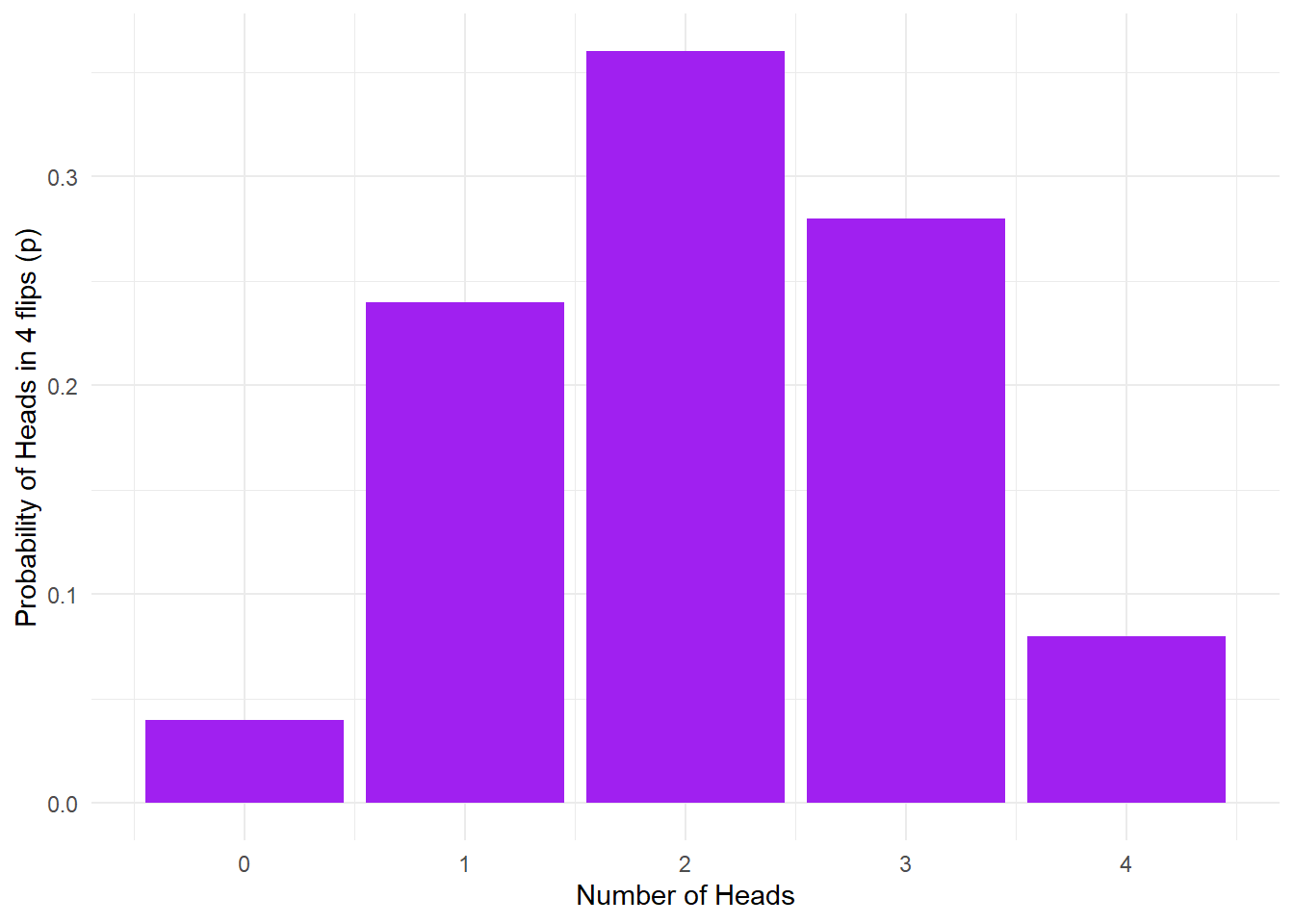
Figure 15.1: No. of heads from iv coin tosses probability outcomes.
Pause here and interpret the above figure
- What is the estimated probability for flipping 0/4 heads? one/iv heads? 2/4 heads? 3/4 heads? four/4 heads?
Unfortunately sometimes this adding will gauge that the probability of an outcome is zero since this outcome never came up when the simulation is run. If y'all want reliable estimates, you demand a bigger sample to minimise the probability that a possible outcome won't occur.
Activity 7: large data
Let'southward echo the Monte Carlo simulation, but with 10,000 trials instead of only l. All nosotros need to do is change due north from fifty to 10000.
heads10K <- replicate(n = 10000, expr = sample(0 : 1, 4, TRUE) %>% sum()) Over again, we'll put the consequence into a table using tibble and summate counts and probabilities of each outcome using group_by() and summarise(). Remember to effort reading your code in total sentences to aid you empathise what multiple lines of code continued by pipes are doing. How would y'all read the below code?
data10K <- tibble(heads = heads10K) %>% group_by(heads) %>% summarise(due north = due north(), p=n/ 10000) Finally, we can visualise this as nosotros did before.
ggplot(data10K, aes(heads,p)) + geom_bar(stat = "identity", fill = "purple") + labs(x = "Number of Heads", y = "Probability of Heads in 4 flips (p)") + theme_minimal() 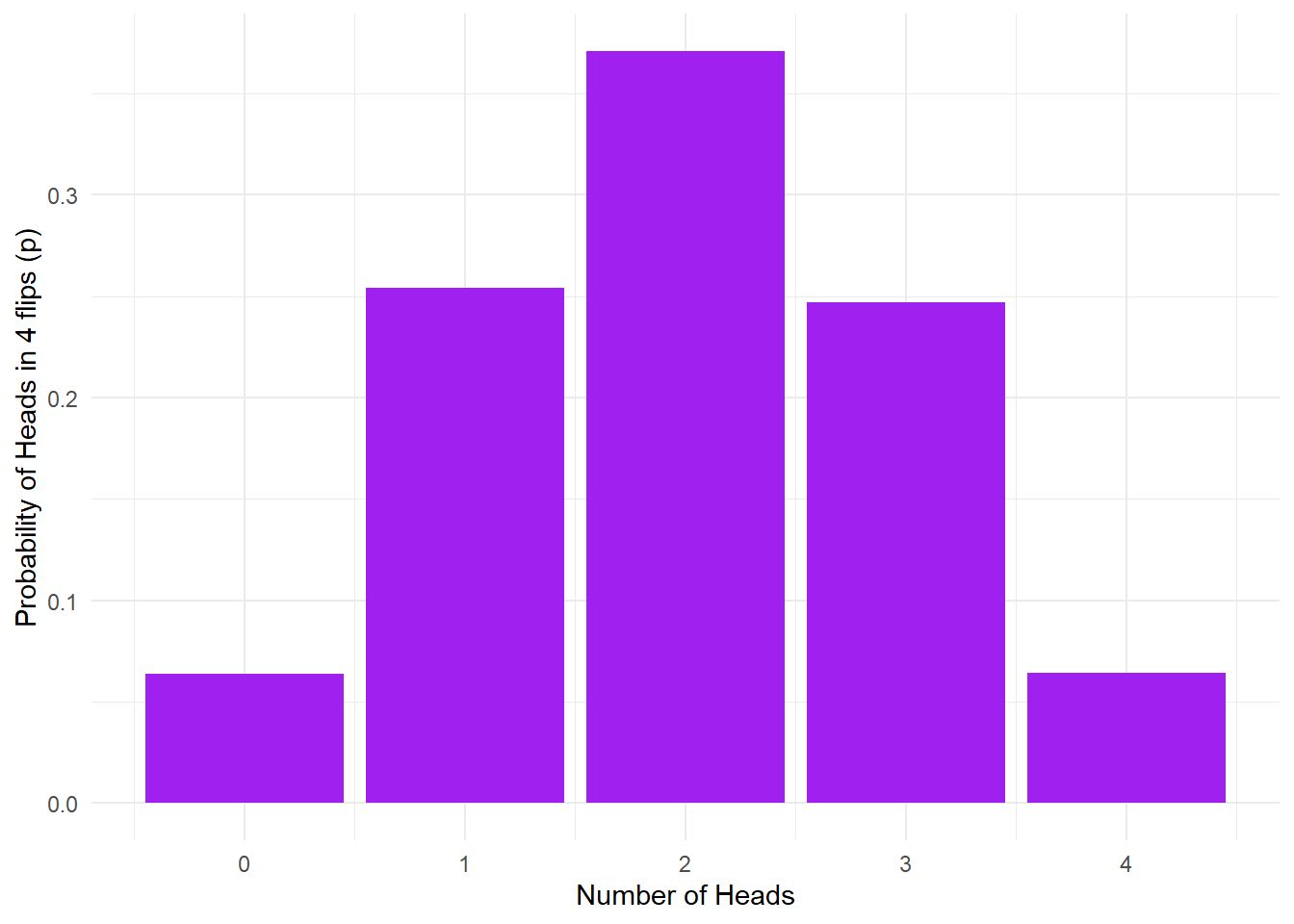
Figure 15.2: 10K money toss probability outcomes.
Using Monte Carlo simulation, we estimate that the probability of getting exactly 1 head on four throws is about 0.25. The above result represents a probability distribution for all the possible outcomes in our experiments. We can derive lots of useful information from this.
For instance, what is the probability of getting two or more heads in four throws? This is easy: the outcomes meeting the criterion are 2, 3, or 4 heads. We can simply add these probabilities together similar so:
data10K %>% filter(heads >= 2) %>% summarise(p2 = sum(p)) ## # A tibble: 1 x 1 ## p2 ## <dbl> ## 1 0.682 Yous can add probabilities for various outcomes together equally long as the outcomes are mutually exclusive, that is, when ane issue occurs, the others tin't occur. For this coin flipping example, this is obviously the instance: you lot can't simultaneously go exactly two and exactly 3 heads as the outcome of a single experiment. Nonetheless, be enlightened that you can't simply add together probabilities together when the events in question are not mutually exclusive: for case, the probability of the coin landing heads up, and information technology landing with the image of the head being in a particular orientation are non mutually exclusive, and can't exist simply added together.
This is the basis of how we can calculate the probability of an event using a known distribution - past simulating a large number of trials nosotros can use this as an gauge for how our data will wait in the real world.
Activity 8: rnorm()
We tin also use R to simulate continuous information that follow a normal distribution using rnorm(). You've actually used rnorm() earlier, all the way back in Intro to R from Psych 1A merely nosotros'll go over it again.
-
nis the number of data points you lot wish to simulate which is the merely required argument forrnorm() -
meanis the hateful that you want your data to have. If you don't provide this statement,rnorm()volition apply a default value ofmean = 0. -
sdis the standard deviation you want your data to have. If you don't provide this argument,rnorm()will employ a default value ofsd = 1.
Copy, paste and run the below code in a new code clamper. This will randomly generate 50 numbers that collectively take a mean of ten and a SD of 2 so store it in the object normal.
normal <- rnorm(n = 50, hateful = 10, sd = ii) You lot can check that the information you accept generated are equally you expected by calculating the hateful and SD of this new variable - you shouldn't expect the values to be exactly 10 and 2 (remember, it's randomly generated), but they should be reasonably close.
## [1] ix.653285 ## [1] 2.185697 Finally, you can visualise your data with a density plot. Try irresolute the number of data points generated by rnorm() from 50 to 500 to 5000 and then come across how the shape of the distribution changes.
tibble(normal = normal) %>% #plough the variable normal into a table then ggplot(aes(normal)) + # create a density plot geom_density(make full = "red") + theme_minimal() 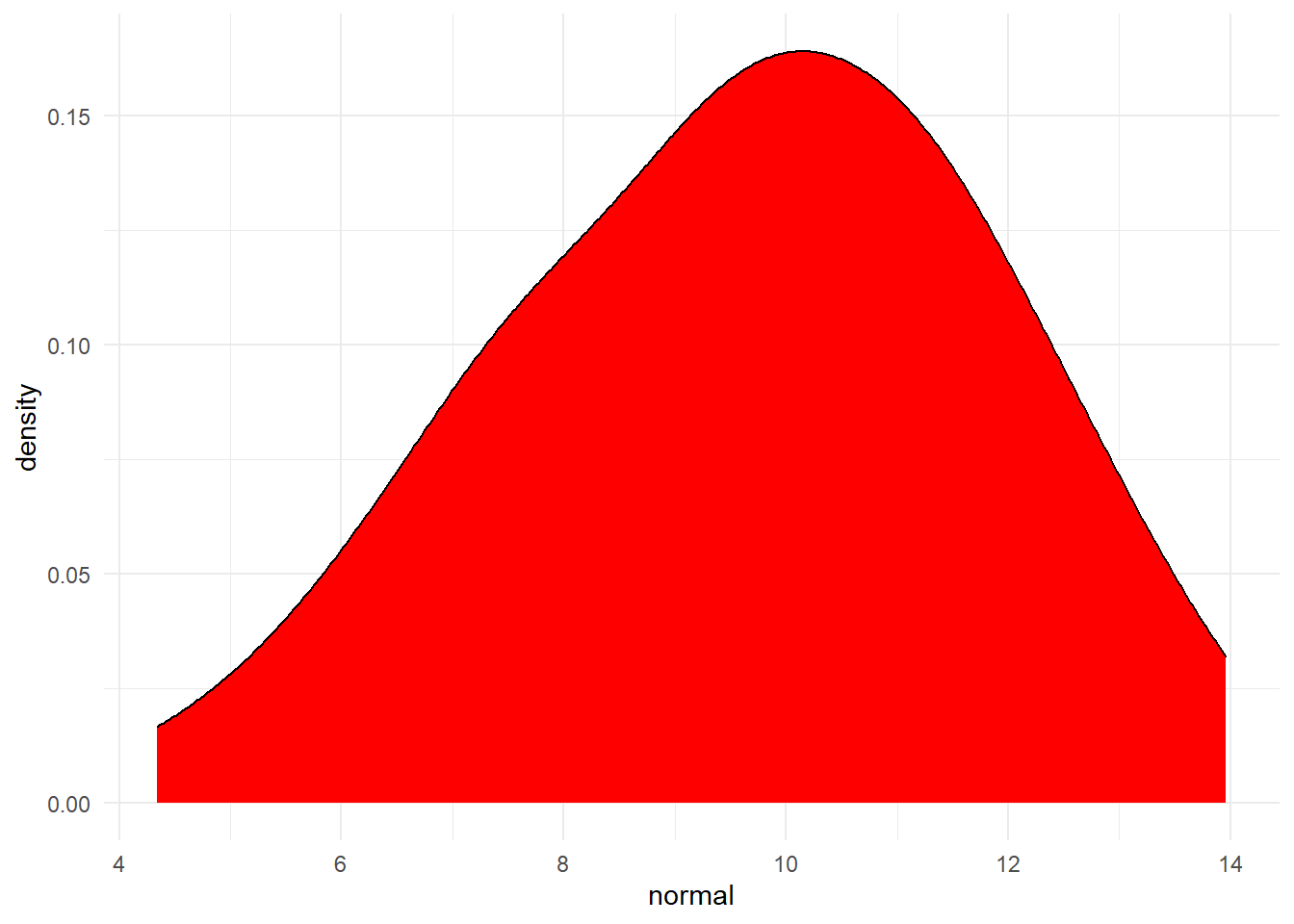
Figure vii.3: Distribution of variable created by rnorm
Activity 9: Simulate a dataset
Finally, nosotros can put all of this together to simulate a full dataset. Let's imagine that we're going to run an experiment to come across whether 120 people will curlicue a higher number on a dice if their IQ is college. This is obviously a stupid experiment but psychology does occasionally do stupid things.
- Offset, allow's create a variable that has all of our field of study IDs. We're just going to assign our participants numerical codes.
subject_id <- 1 : 120 # create a variable called subject_id that has the numbers one to 120 in it Then we're going to create a cavalcade for gender using a new just simple function rep which stands for "repeat." The below code volition create a variable that repeats "man" 40 times, then "women" 40 times, then "non-binary" 40 times.
gender <- rep(10 = c("human being", "woman", "nonbinary"), each = twoscore) Adjacent, let'due south simulate them all rolling a die in one case using sample().
rolls <- sample(x = 1 : 6, size = 120, replace = Truthful) Then, permit's simulate their IQ scores. IQ scores are standardised so that overall, the population has an average IQ of 100 and a SD of 15 and then we tin use this information to simulate the data with rnorm().
iq <- rnorm(n = 120, mean = 100, sd = 15) Finally, we can run up all these variables together into a tabular array.
sim_data <- tibble(subject_id, gender, rolls, iq) Now that we've got our faux data we could write code to analyse it even earlier we've collected whatsoever real information which volition non only salvage us time in the futurity, but will help united states programme our analyses and nosotros could include this lawmaking in a pre-registration document.
For example, you could create a plot of IQ scores for each dice roll (retrieve these are non existent data…)
sim_data %>% mutate(rolls = as.factor(rolls)) %>% ggplot(aes(x = rolls, y = iq, fill up = rolls)) + geom_violin(trim = Imitation, alpha = .half-dozen, evidence.legend = FALSE) + geom_boxplot(width = .two, show.legend = FALSE) + scale_fill_viridis_d(option = "Due east") + theme_minimal() + labs(ten = "Result of dice roll") 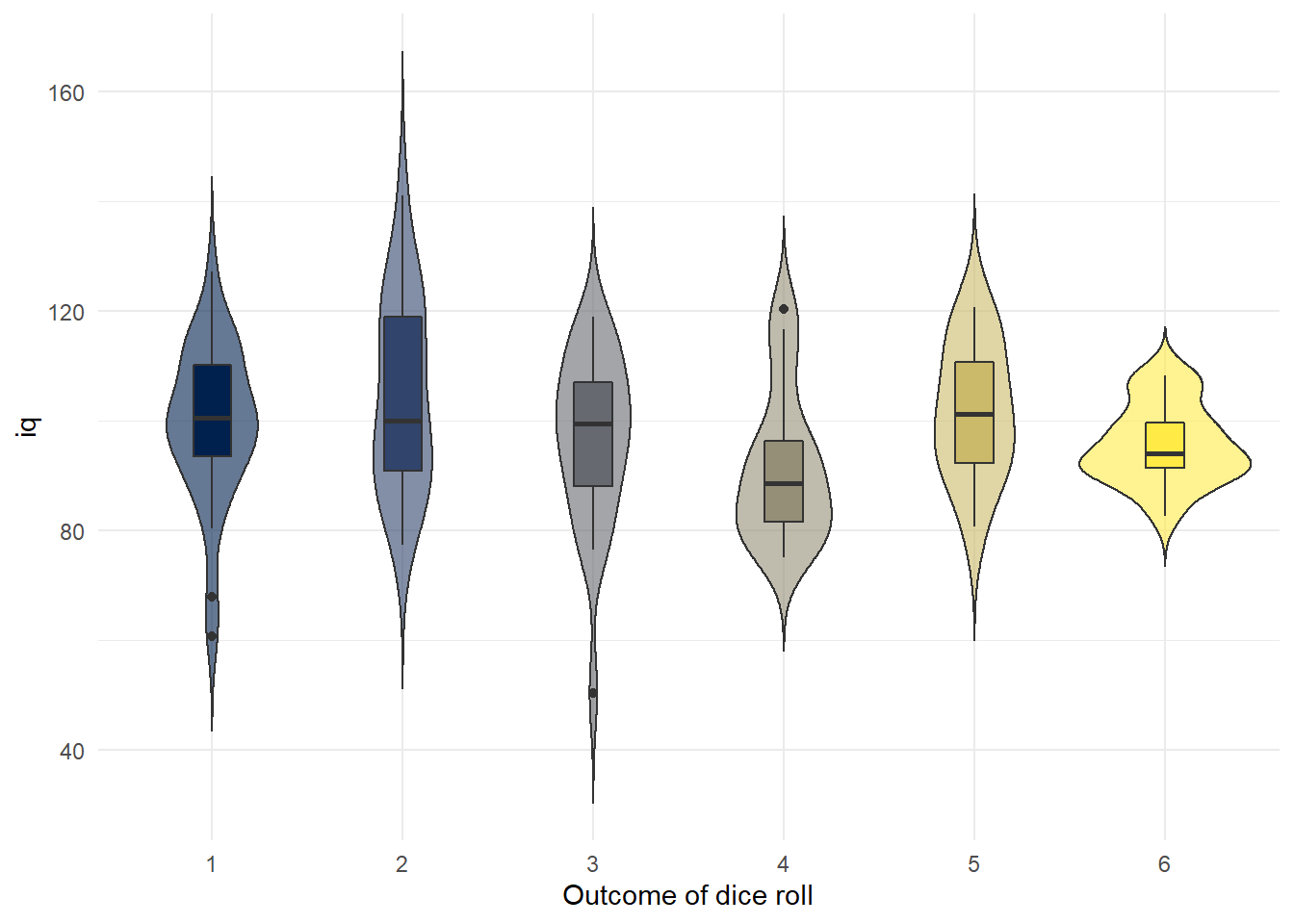
Figure vii.7: Boxplot of IQ scores grouped past what each person rolled on the die
Finished!
The terminal Data Skills activeness is to analyse your group project data which means in terms of new stuff to larn, we're done! In Psych 1A and 1B, we've tried to give you lot a solid introduction to common data skills you'll need in order to conduct your ain inquiry. Even if yous don't intend to keep with psychology or quantitative research in the future, nosotros promise that y'all're proud of the skills you've learned. For some of you, R might not take been your favourite bit of the course, but you should be very proud of what you've achieved and with such a diverse grade we hope you can see that programming isn't an innate skill that only certain people can larn. It just have a a chip of work, some (hopefully) helpful teaching materials, and a lot of swearing at the error messages.
Coin Toss Probability if Head Roll Die if Tail Flip Again in R
Source: https://psyteachr.github.io/ug1-practical/simulation.html